刚刚(11月3日),国家科学技术奖公布。由复旦大学数学科学学院雷震教授、周忆教授共同完成的项目《不可压流体方程组的非线性内蕴结构》,解决了流体方程组解的整体适定性之系列关键问题,获得自然科学奖二等奖。

雷震的办公室安静而空旷,空荡荡的书桌、沙发和书橱。唯一引人注目的,是办公桌对面黑板中央的那个一般人看不懂的轴对称Navier-Stokes方程组:
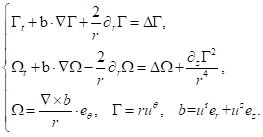
“这个方程组我已思考了十余年了。每天我都要面对它,想要找到一条正确的破解之路。” 雷震站在黑板前凝视,间或拿起粉笔在一旁写写画画。悄无声息之间,一场数学思维的风暴已在激荡。
获奖的雷震,经历了短暂的喜悦,很快就投入到新的科研工作中去了。在那片抽象深奥而又人迹罕至的数学高原,还有许许多多的高峰矗立在前方:轴对称不可压Navier-Stokes方程组解的正则性,密度具正下界的可压缩Navier-Stokes方程组有限能量解的奇性,Schrodinger方程与二维不可压Euler方程组解的高阶范数关于时间的增长下界,不可压流体方程组的弱解......
学术人生,贵在坚持

在复旦读博阶段,雷震进入了非线性波动方程的研究领域,弹性力学方程组是其典型代表之一。1986年,两位美国科学院院士Christodoulou和Klainerman在零条件和小初值的条件下取得了突破性的研究进展,各自独立地证明了具洛伦次不变性的三维非线性波动方程解的整体适定性。2000年,日本数学家Agemi和美国数学家Sideris克服了洛伦次不变性缺失的困难,成功地将上述理论发展到力学基本方程组之一的可压缩弹性力学方程组,在非线性项满足零条件的假设下各自独立地证明了三维情形平衡态附近经典解的整体适定性。2001年,满足零条件的两维非线性波动方程也被法国数学家Alinhac解决。这一年是雷震入读研究生的第一年,在这个研究领域,他所面对的正是二维弹性力学方程组平衡态附近经典解的整体适定性这一关键而困难的最后堡垒。然而,直至博士毕业,雷震也未能攻克这一堡垒。
博士毕业后,雷震继续专注于不可压情形的流体力学方程组解的数学理论研究,特别是二维情形的弹性力学方程组和三维情形的Navier-Stokes方程组解的整体适定性研究。他发现不可压流体都有一种非线性的内蕴强退化结构,这种结构会导致非线性项的稳定性增强。在此基础上,雷震提出了“强零条件”的概念,把这种新发现的非线性内蕴强退化结构数学化,进而解决了长期以来困扰人们的多个关键困难,最终建立了二维情形弹性力学方程组平衡态附近经典解的整体适定性理论(于2016年发表)。作为这一成果的延续,雷震与其博士生蔡圆及合作者林芳华、Masmoudi近期进一步建立了粘弹性流体力学方程组关于时间整体成立的粘性消失理论。
在千禧奖问题之一的Navier-Stokes方程组(NS)解的整体适定性研究领域,雷震与侯一钊合作建立了首个满足能量等式的三维模型并揭示了NS中对流项具有出人意料的稳定性机制,并与张旗合作建立了轴对称情形的解产生有限时间奇性的判别法进而刻画了潜在奇性解破裂的速度。近期,雷震与任潇(雷震的在读博士研究生)及张旗合作进一步得到了关于轴变量周期的古代解的刘维尔定理。
谈起这些成绩,雷震说经历的失败远多于成功。“对我而言,人生就是一个个方程组,成功就是把它们解出来。”与其说失败,他更愿把科研比作冲浪或滑雪,始终是一种颠簸起伏的状态。这就是一种生活,是一种可以去享受的生活状态。“你经常会感到走投无路,但第二天又柳暗花明。你兴奋得整晚睡不着觉,早晨却发现又做错了。你彻底绝望时,又发现一丝曙光。就这样周而复始。”雷震笑言,科研不总是一个可预期的行为,研究时常起起伏伏,永远都在成功的路上,但只要坚持,就肯定会有结果。
如今,写在黑板上的这个轴对称Navier-Stokes方程组,是雷震努力攀登的另一座高峰。“这是Navier-Stokes方程组的一种特殊情形,是当今世界上偏微分方程研究领域最核心的问题之一。它已经融入我的生活,我必须去面对它”。雷震如今每天都跟这个方程组打个照面,天天睡觉前都要想一想。看似毫不费力的工作方式背后,是常人无法想象的坚持。他说,作为一名科学家,必须和科研融为一体,进入状态的生活才是幸福的。
被时代推着跑的有责任感的教授
“我们这代人,很多时候是被这个时代推着跑的。”雷震坦言,他的理想是在求学与成长的过程中一步步树立起来的,一个人能走多远,不仅跟个人努力有关,更与时代大背景有关。
2014年,雷震在普林斯顿高等研究院
雷震曾在美国加州理工学院从事博士后研究,并曾为普林斯顿高等研究院member及哈佛大学访问学者。他当时有机会留美工作,但确选择了回国。“中国人是有大国情怀的。成为一流学者后,你会开始为这个国家、这个民族的未来去思考。所以你的天地很广阔,有很多事情去做,甚至会发现你的事业才刚刚开始。”
“责任感”这个词,经常出现在雷震口中,贯穿于他的个人发展道路,也贯穿于他的教学育人的全过程。他重视培养学生的家国情怀,要求学生做世界一流的研究。“什么研究该做、什么文章该写,你们需要好好考虑。你们可以发很漂亮的文章、找很好的工作,但作为复旦大学毕业的偏微分方程学者,你们对中国偏微分方程的发展是负有责任的。”
虽然是教数学,但雷震常跟学生聊学术,也聊生活、聊社会。面对年轻人的发展困惑,他教导学生们不要局限于个人利益得失,要把为祖国和社会作贡献作为一种崇高的追求。“即便是做数学理论研究,也要围绕生产生活中的问题开展,要扎根中国实际,为国家、为社会发展服务。”他说。
鼓励、陪同学生读经典论文,却不主张学生轻易发论文

雷震作学术报告
科研之外,雷震一直为本科生教授《数理方程》课程,积极推动复旦数院拔尖人才计划和专题讨论班的建设,是教育部“基础学科拔尖学生培养计划”实施十周年优秀导师奖获得者。
在“拔尖计划”成员、2018级博士生任潇的记忆中,雷老师授课风格既严谨又幽默,经常举一些生动形象的例子帮助学生理解,同时不拘泥于课本,会补充很多学术前沿的研究思想和方法。“他会告诉我们真正学好一门课的方法是什么,既进行有效的学术指导,也有意培养学生的自主探索能力。”任潇说。
对参与“拔尖计划”的学生,雷震尤其注重培养方式,非常强调培养学生的眼界和品味,鼓励他们从思想和方法上去突破与创新。“这类学生是国家的战略资源。我通常从他们大三、大四时开始带领他们接触学科最前沿、最关键的研究课题。”
作为本科生进入学术前沿的第一步,雷震会选择相关研究领域最经典论文让他们研读,会花一个学期的时间陪他们去读一篇论文,“读到从整体目标到现有进展及每一个环节都要比作者更懂”,这对本科生来说显然有相当的难度。但扎实地经过了的这一步科研训练,本科生将具备与相关领域顶尖数学家较自由的沟通交流的能力,而这对他们的进一步成长意义重大。
另一方面,雷震并不主张甚至反对学生轻易发表SCI论文。“年轻人急于成功,若养成有一些发现就很想发论文的心态和习惯,短期看会获得一些知名度,但是长远看来,往往会成为其进一步成长的巨大障碍。”
日常教学外,雷震常给研究生上专题讨论课。只要有时间,他就会将博士生、博士后聚在一起,围绕大家共同关心的问题深入讨论。讨论课常常持续半天甚至一整天,一周三四次,即便最忙的时候也保持至少一周一次的频率。一篇文章,通常要被讨论20个半天以上。
“让我来想想”——雷震的这句口头禅让学生印象深刻。他很在意培养研究生的自主探索意识。“无论你读谁的论文,都要从头怀疑到尾,每一个环节都要挑战他,甚至怀疑他的研究目标。不能因为作者很有名你就俯首称臣,就被牵着鼻子走。”

雷震与学生探讨问题
每当学生报告新命题,雷震就会说“让我来想想”,随后拿起粉笔,在黑板上开始推演,直到无法推进下去,才会去分析作者是如何证明的。“雷老师会亲身示范怎样去学习、研究。如果没有这个过程的话,我们自己可能很难找到头绪。”任潇觉得,这种独立推演思维,让自己获益匪浅,“往往能够看到问题的本质、学到前人研究工作的精髓”。
他要培养三、五个能承担起国家责任的好学生

雷震与学生们合影
忆起当年在复旦读博的日子,雷震强调他得到了许多大师的指导。李大潜院士、洪家兴院士、陈恕行院士……耳濡目染之间,雷震学到了许多治学为人的道理。“榜样的力量是最大的。他们让我从内心深处确立了自己的人生方向。”雷震说。
与雷震此次一同获奖的周忆教授是其博士导师。“周老师是一个真正的学者,为人谦虚大度,我的很多思想和技术都是从周老师那里学过来的。”雷震说,两人的合作多年来从未间断。
经过几代人的不断努力,复旦数院目前已在许多研究领域达到了世界先进水平。在雷震看来,数院一脉相承的精神,其实在数学之外——要为中国的数学做贡献,为国家的发展贡献力量。“复旦之所以能凝聚一批人在这里传承,不为外界所扰,正是因为这种对国家和民族的使命感。”
作为复旦中青年数学家的中坚力量的一份子,雷震如今最大的心愿,就是培养三五个能够承担起国家责任的好学生。
“一名教授应尽量培养出一个比自己强的学生;如果能培养出两个比自己强的学生,那他对社会的贡献就算很大了。我对自己的期望可能更高一点”。雷震笑言。



 地址:上海市杨浦区邯郸路220号
地址:上海市杨浦区邯郸路220号 邮编:200433
邮编:200433 电话:021-65642222
电话:021-65642222
